图解数据结构之二叉堆

(Updated: )
, ,

介绍

定义

二叉堆是一颗二叉树，即每个节点只有一个父节点并且每个节点最多有两个子节点的树形结构。 二叉堆分为最大堆和最小堆，如果堆中的任意一个节点的值都大于等于它的子节点，称为最大堆。如果堆中的任意一个节点的值都小于等于它的子节点，称为最小堆。

下图这颗二叉树就是一个最大堆，树中每个节点都大于等于该节点的子节点：

完全二叉树

二叉堆是一颗完全二叉树，即当一颗子树存在右节点的时候这颗子树一定存在左节点。我们会看到这颗二叉树的节点都是从左往右连续排列的。对于完全二叉树更加严谨的定义为：

若设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第h层所有的结点都连续集中在最左边。

下图是一颗完全二叉树，树中的节点都是从上到下从左至右一个节点一个节点依次存放：

基本操作

  • 插入节点：向二叉堆中插入一个节点。
  • 取出最大（最小）节点：取出二叉堆的根节点。

应用

  • 优先队列
  • 堆排序
  • 解决top K问题

具体实现

下面的具体实现都是以最大堆为例，即二叉堆的根节点大于等于它的所有子节点。最小堆的操作跟最大堆是一样的，只是节点间的比较关系不同而已。

存储

由于二叉堆是一颗完全二叉树我们可以使用一个数组来存储，数组的每个元素就是二叉堆中的各个节点。这是因为完全二叉树的节点从左至右是连续的。如果不是完全二叉树，节点在数组中的索引就会离散不连续便会浪费内存空间。当要存储有N个节点的二叉堆时，一般会用长度为N+1的数组来存储这颗二叉堆。数组索引为1元素就是二叉堆的根节点。索引0的位置就空着不用，这是为了方便计算每颗子树的子节点和父节点的索引。

如果树的某个节点在数组中的索引是k那么：

  • 该节点的父亲节点索引：k / 2 (向下取整)
  • 该节点的左子节点索引：2 * k
  • 该节点的右子节点索引： 2 * k + 1

下图树中每个节点上的数字表示节点在数组中的索引，节点里的数字表示节点所对应的元素值。

这棵树在数组中存储结构为：

其中索引为3的节点它的父节点和子节点的索引为：

  • 父节点索引：3 / 2 = 1（向下取整）
  • 左子节点索引：2 * 3 = 6
  • 右子节点索引：2 * 3 + 1 = 7

二叉堆初始化代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class BinaryHeap {
private:
    // 存放二叉堆的数组
    int *container = NULL;
    // 容量，也就是最多能存放多少个节点
    unsigned int capacity = 0;
     // 二叉堆的大小
    unsigned int size = 0;
public:
    BinaryHeap(unsigned capacity) {
        assert(capacity > 0);
        // 初始化存放二叉堆的数组
        this->container = new int[capacity];
        this->capacity = capacity;
    }
};

索引计算代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
// 左子节点索引
unsigned calculateLeftChildIndex(unsigned index) {
    return index * 2;
}
// 右子节点索引
unsigned calculateRightChildIndex(unsigned index) {
    return this->calculateLeftChildIndex(index) + 1;
}
// 父节点索引
unsigned calculateParentIndex(unsigned index) {
    return index / 2; // C++除法如果两边都是整型的话默认向下取整
}

插入节点

插入节点就是往堆中新增一个节点，同时不能破坏二叉堆的对应。

插入节点时，先把要插入的节点添加到二叉堆的堆尾（等价于在数组末尾新加一个元素）。此时二叉树中新插入的这个节点可能比它的父节点还要大，现在的这颗二叉树就不再满足最大堆的定义。需要把该节点与它的父节点交换位置。交换后新的父节点还是有可能比这个新的父节点的父节点还要大，那么就再重复一次之前的操作，这样一层一层向上移动直到堆顶或者遇到的节点不再比它的父节点大为止。整个交换节点的操作叫做shiftUp，当该操作完成之后这颗二叉树又重新满足最大堆的定义。

往下图左边的二叉堆的堆尾插入节点10，得到右边树的样子。发现新加入的节点10比它的父节点6还要大，此时右边树就违背了二叉堆的定义，不再是一个二叉堆。所以我们需要对新加入节点的位置（也就是节点10所在的位置）做shifUp操作：

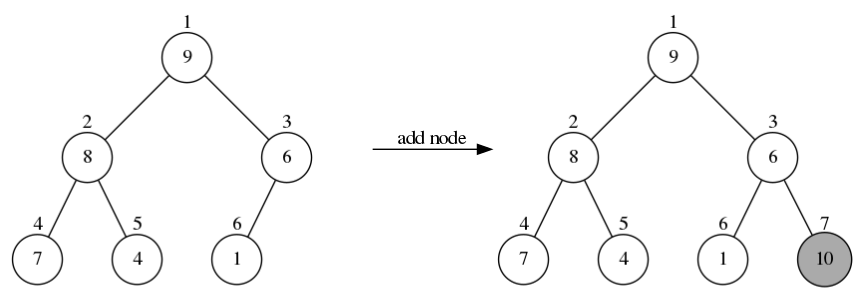
下图左边的树中节点10比它的父节点6要大，所以它们需要交换位置，得到右边树：

下图左边的树中节点10仍旧比它的父节点9要大，所以它们再次交换位置，得到右边树：

节点10最终被移到了根节点，观察树中的任意一个节点都大于它的子节点，这样一来整个二叉树又重新满足了二叉堆的定义。整个修复二叉树的过程就是shiftUp操作。

插入节点实现代码：

1
2
3
4
5
6
void insert(E element) {
    assert(!this->isFull());
    this->container[this->size] = element;
    this->shiftUp(this->size);
    this->size ++;
}

shiftUp实现代码：

1
2
3
4
5
6
7
8
void shiftUp(unsigned currentIndex) {
    unsigned parentIndexOfCurrentIndex = this->calculateParentIndex(currentIndex);
    while ((index > 1) && this->compare(this->container[index], this->container[parentIndexOfCurrentIndex])) {
        swap(this->container[index], this->container[parentIndexOfCurrentIndex]);
        currentIndex = parentIndexOfCurrentIndex;
        parentIndexOfCurrentIndex = this->calculateParentIndex(currentIndex);
    }
}

while中的index > 1表示该索引不是堆顶索引，this->container[index] >= this->container[parentIndexOfCurrentIndex / 2]表示该节点大于它的父亲节点。只要同时满足这两个条件就交换位置，同时把索引设成原来节点的父节点，一样一层一层向上移动，直到不满足这两个条件中的任意一个就退出。

删除节点

从二叉堆中删除接点时，每次只能删除堆顶位置的节点。对于最大堆就意味着每次删除堆中最大的那个节点。如果用堆来实现优先队列，那么从堆中删除一个节点，可以理解为从堆中取出优先级最高的节点。

把堆顶的节点删除之后，再把堆尾的节点移到堆顶的位置。产生的新的二叉树中堆顶的节点可能比它的子节点小，此时这颗二叉树就不再满足二叉堆的定义。需要把新的堆顶的节点与它子节点中最大的那个节点交换位置。交换后新的子节点还是有可能比这个新的子节点的子节点要小，那么就再重复一次之前的操作。这样一层一层向下移动直到遇到的节点不再比它的子节点小为止或者到了堆的底部。整个交换节点的操作叫做shiftDown，当该操作完成之后这颗二叉树又重新满足最大堆的定义。

当从左边树中删除接点时，先找到堆顶位置的节点10，然后把它删除之后得到右边树：

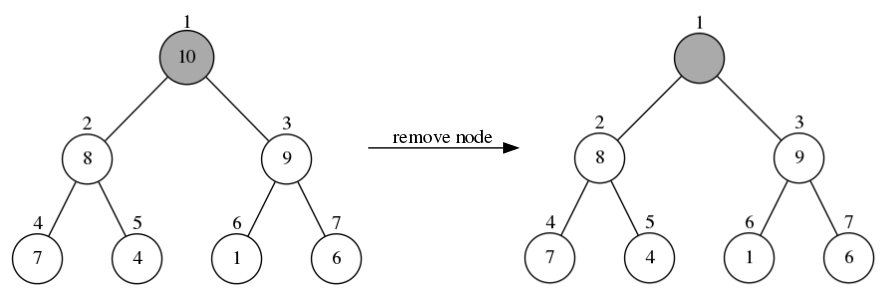
接下来把左边树中堆尾位置的节点6移到堆顶的位置，得到右边树：

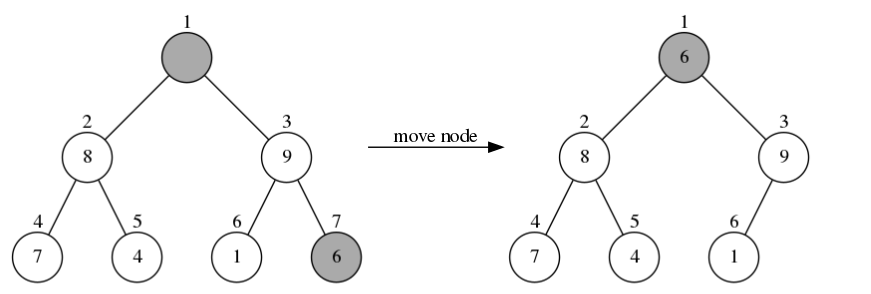
此时左边树中堆顶位置的节点6比它的两个子节点还要小，就让该节点与它子节点中最大的那个节点交换位置。它的两个子节点分别是8和9，最大的子节点是9，所以节点6与节点9交换位置，交换之后得到右边树：

完成上面的操作之后，节点6的子节点中没有比它大的节点，所以终止操作，最终得到下图中的树。它又重新满足了二叉堆的定义。

具体代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
void shiftDown(unsigned currentIndex = 0) {
    unsigned leftChildIndexOfCurrent = this->calculateLeftChildIndex(currentIndex);
    // 判断当前节点的左子节点的索引是否超过了数组的大小,如果超过了,就代表该节点没有左子节点.
    while(this->getSize() >= leftChildIndexOfCurrent) { // 如果该节点存在左子节点
        unsigned maxChildIndexOfCurrent;
        unsigned rightChildIndexOfCurrent = calculateRightChildIndex(currentIndex);
        if ((this->getSize() >= rightChildIndexOfCurrent) && (this->container[rightChildIndexOfCurrent] > this->container[leftChildIndexOfCurrent])) { // 如果该节点存在右子节点并且右子节点比左子节点大
            maxChildIndexOfCurrent = rightChildIndexOfCurrent;  // 把最大的子节点设为右子节点.
        } else {
            maxChildIndexOfCurrent = leftChildIndexOfCurrent; // 否则就把最大的子节点设为左子节点.
        }
        if ((this->container[currentIndex] >= this->container[maxChildIndexOfCurrent])) { // 如果当前节点大于等于它最大的子节点,那么就没有打破最大堆的定义,所以直接break掉就好了.
            break;
        }
        // 如果当前节点存在一个子节点比它还要大,那么就交换这2个节点的位置
        swap(this->container[currentIndex], this->container[maxChildIndexOfCurrent]);
        // 把当前循环的索引设为新的根节点的索引然后继续向下检查.
        currentIndex = maxChildIndexOfCurrent;
        leftChildIndexOfCurrent = this->calculateLeftChildIndex(currentIndex);
    }
}

该代码实现思路就是先判断当前节点是否存在左子节点。然后判断当前节点是否存在右子节点。如果存在的就找出这两个子节点中最大的子节点。然后再判断当前节点是否大于等于它子节点中的最大的子节点如果成立就退出，因为并没有违背最大堆的定义。不成立的话就说明当前节点存在一个子节点比它还要大，那么就将当前节点和它最大的那个子节点交换位置，同时把当前循环的索引设为新的根节点的索引然后继续向下检查。

构造二叉堆

把N个元素构造成一个二叉堆。

把N个元素构造成一个二叉堆一般有两个办法：

  • 第一个办法是通过二叉堆的插入节点操作依次把每个元素插入至堆中。
  • 第二个常用的办法是把这N个元素存入一个数组，此时可以把这个数组想象成一个完全二叉树，但是它还不是一个二叉堆。然后对这个数组的最后一个元素开始依次往回做shiftDown操作，这一步的目的是为了保证二叉堆中每颗子树都满足二叉堆的定义。但是我们发现如果某个节点是一个叶子节点的话那么它根本不需要做任何操作，因为它没有子节点，即使对这个节点做了shiftDown操作也等于没做。所以后来优化之后我们可以从最后一个拥有子节点的节点开始往回做shiftDown。最后一个拥有子节点的节点也被称为非叶子节点，它的索引就是堆尾节点的父节点的索引。这个方法被称为heapify。

heapify实现：

1
2
3
4
5
6
heapify(int *arr, unsigned size) {
    // size 就是堆尾的位置，它的父节点就是最后一个拥有子节点的节点
    for (int i = this->calculateParentIndex(size); i >= 1; i --) {
        this->shiftDown(i);
    }
}

兼容最小堆和最大堆

有时候我们需要使用最小堆，但有时候我们又需要使用最大堆，但是它们两个往往代码几乎一模一样只是比较符号的方向不同，为了复用代码，我们只需要给二叉堆设定一个比较方法即可，比如在初始化最大堆的时候给它传入一个方法，这个方法就用来做比较操作。 当二叉堆中需要做比较的时候调用该方法就好了。

如果是一个最小堆,我们的比较方法如下：

1
2
3
bool compare(int a, int b) {
    return a < b;
}

例如堆中相应地方调用的时候：

1
2
3
if (this->compare(this->container[calculateRightChildIndex(index)], this->container[calculateLeftChildIndex(index)])) {
// ........
}

说明

本文对堆的定义和常用操作做了阐述，文中的代码使用了C++，数据结构与算法的重点在于思想和逻辑所以大家完全可以在了解了算法思想之后用自己熟悉的任意一门语言来实现。后面还会出一篇关于二叉堆应用和复杂度分析的文章。

源代码

具体实现：

https://github.com/acodercat/cpp-algorithms/blob/master/include/binary_heap.h

调用样例：

https://github.com/acodercat/cpp-algorithms/blob/master/src/examples/binary_heap.cpp

仓库代码中的二叉堆是从索引0开始的，所以在父节点索引计算上会有不同。