SICP笔记-程序设计的基本元素
在程序设计中,我们需要处理两类要素:过程和数据。数据是一种我们希望去操作的
东西,而过程就是有关这些操作的规则描述。
每一种强有力的语言都为此提供了三种机制:
- 基本表达形式:用于表示语言所关心的最简单的个体。
- 组合的方法:通过它们可以从较简单的东西除法构造出复合的元素。
- 抽象的方法:通过它们可以为复合对象命名,并将它们当做单元去操作。
任何强有力的程序员设计语言都必须能表述基本的数据类型和过程,还需要提供对过程和数据的组合和抽象的方法。
表达式
把表示基本过程的表达形式(如+,-,*,/),将表示数的表达式组合起来,形成复合表达式,以表示求把有关过程应用与这些数。
例如:
1 | (+ 100 1) |
像上面的表达式称为组合式。括号里最左的元素称为运算符,其他元素称为运算对象。
将运算符放在所有运算对象的左边,这种形式称为前缀表示。它的优点之一就是可以完全适用于可能带有任意个实参的过程。
例如:
1 | (+ 100 1 100) |
前缀表达式的另外一个优点在于它可以出现组合式嵌套,也就是允许组合式中的元素又是一个组合式。
例如:
1 | (+ (* 10 10 ) (+ 10 10 )) |
命名和环境
程序设计语言会提供一种通过名字去使用计算对象的方式,将名字标识符称为
变量,它的值也就是它所对应的那个对象。
在scheme里通过define(定义)的方式完成,例如:
1 | (define size 2) |
会导致解释器将值2与名字size关联,一旦名字size和2关联之后,我们就可以通过这个名字去引用值2了:
1 | (* size 2) |
define就是scheme里最简单的抽象方法,它允许我们用一个简单的名字去引用一个组合运算结果。例如:
1 | (define pi 3.1415926) |
ciroumference的结果是 62.8318,它就是组合式 (* 2 pi radius)的结果。通过这种方式,我们可以不用在每次使用某个组合式的时候都记住该组合式背后的具体实现细节,而是通过一个名字与组合式进行关联,然后就可以直接使用名字来引用某个组合式。
我们将值与符号关联,而后又能提取出这些值,这意味着解释器必须维护某种存储能力,以便保持有关的名字与值之间的对应关系。这种存储被称为环境。
组合式的求值
要对一个组合式求值,需要做:
- 对该组合式的各个子表达式求值。
- 把最
左子表达式(运算符)所表示的过程应用在相应的实际参数上。实际参数也就是其他子表达式的值。
例如:
1 | (* (+ 2 3) (+ 4 5)) |
这个组合式有两个子表达式,分别是(+ 2 3)和(+ 4 5)。先计算出这两个子表达式的值为5和9,然后把左子表达式(运算符)所表示的过程应用在相应的实际参数上,也就是把*(乘法)过程应用到5和9上,最终得到结果45。
再考虑一个稍微复杂一点的例子:
1 | (* (+ 2 (* 4 6)) |
这个组合式是一个嵌套结构,也就是该组合式的子表达式仍然是一个组合式。此时我们需要对组合式的每个子表达式执行同样的求值过程。因此这一求值过程是递归的。我们可以用树形结构来表示整个求值过程。上面的这个组合式用树形结构结构就可以表示成:
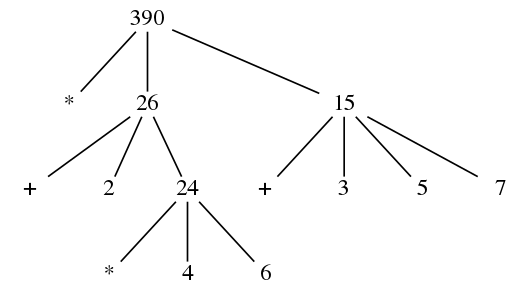
树中的每个节点可能是数、内部运算符或者其他名字,处理这些基础情况的方式如下规定:
- 数的值就是它们所表示的数值。
- 内部运算符的值就是能完成相应操作的机器指令序列。
- 其他名字的值就是在环境中关联于这一名字的那个对象。
复合过程
define除了可以定义值以外,还可以定义过程。
例如:
1 | (define (sequare x) (* x x)) |
上面代码定义了一个名字叫sequare的过程,这个过程用来计算一个数的平方。这样就可以通过sequare来调用该过程。
对sequare进行调用:
1 | (sequare 20) |
过程定义的一般形式:
1 | (define (<name> <formal parameters>) <body>) |
其中<name>是过程的名字,可以使用过程名对过程进行调用。 <formal parameters>是过程中需要的参数叫做形参,形参会被调用时候的实参所替换。<body>是一个表达式,这里也可以对其他过程进行调用。
可以通过简单的过程来构建复杂的过程,例如两个数的平方和(x^2 + y^2)就可以被定义成:
1 | (define (sum-of-sequares x y ) (+ (sequare x) (sequare y))) |
对sum-of-sequares进行调用:
1 | (sum-of-sequares 3 4) |
过程也被称为黑盒抽象,也就是过程的实现细节对使用者来说是一个黑箱。使用者在使用某个过程时无需知道该过程的具体实现。例如在使用Lisp解释器自带的+加法过程时,无需知道其内部的实现方式,使用者只需要知道该过程可以完成加法操作即可。由此以来我们就可以基于多个已有的过程去构建其他复杂的过程。
过程应用的代换模型
正则序
正则序求值过程是首先对运算符和各个运算对象求值,然后将得到的过程应用与得到的实际参数。
当我们对之前定义好的sum-of-sequares求平方和过程进行如下调用时:
1 | (sum-of-sequares 3 4) |
首先取出sum-of-sequares的主体:
1 | (+ (sequare x) (sequare y)) |
然后将x和y分别代换成实际参数3和4得到:
1 | (+ (sequare 3) (sequare 4)) |
再将过程sequare做相同的步骤,也就是把实际参数代换到过程的主体部分:
1 | (+ (* 3 3) (* 4 4)) |
然后再对乘法过程进行代换求值:
1 | (+ 9 16) |
最后对加法过程进行代换求值,得到最终结果:25。
应用序
应用序求值是先不求出运算对象的值,直到实际需要它们的时候再去求值。
同样我们对之前定义好的sum-of-sequares求平方和过程进行如下调用:
1 | (sum-of-sequares (+ 5 1) (+ 5 2)) |
当按照应用序求值时,逐步对每个过程进行展开:
1 | (+ (sequare (+ 5 1)) (sequare (+ 5 2))) |
然后进行求值规约:
1 | (+ (* 6 6) (* 7 7)) |
最后得到最终的求值结果:85。
在求值过程中发现分别对(+ 5 1)和(+ 5 2) 求值了两次,所以应用序求值会导致重复求值。所以Lisp采用正则序对过程进行求值来避免重复求值的问题出现。